Excel to R: The Analysis ToolPak

A useful, but often overlooked Excel feature is the Analysis ToolPak. It’s useful because it packages about 20 commonly used statistical functions in a format that is very easy to use. It gets overlooked because it has to be activated through the Excel Options dialog before it even becomes visible.

If the Analysis ToolPak is new to you you will find it in the Data segment of the Excel Tool Ribbon. If you already use it and you are In the process of extending your analysis repertoire to include R, you may just be looking for a guide that shows how to do ToolPak tasks in R. Either way, this post fills a gap with a quick mapping from Excel to R of the five most commonly used functions in the Analysis ToolPak.

Descriptive Statistics

Centre, spread and shape are probably the three things people most often want to know about a dataset. Both Excel and R offer quick tabulations of statistics that supply answers. In Excel, the Descriptive Statistics dialog sets options for selecting the data, output location and which statistics to present, including a confidence interval for the mean. In this case the dataset lists tips received in a restaurant over a period of several weeks; the setup dialog and the result are shown below.

The closest R equivalent is probably the describe function but the collection of statistics it delivers can vary depending on the package that has been activated for basic statistics. The best match to the Excel output probably comes from the psych package as shown here:

The describe function output didn’t include the confidence interval for the mean, so I had to run it separately using the t-test function. That gave me a full description of the statistical test – maybe more information than I want but it got the job done.

Histograms

A Histogram is a quick way to visualize the information that the descriptive statistics provide. Continuing with the tips dataset, the Excel dialog produces both a frequency table and a chart:

To get this I had to decide up-front how many bins I wanted and calculate the boundary values for each. Excel did the rest, giving me both the frequency table and the chart output.

The R equivalents produces this chart using options set within the ggplot function:

The chart specification includes the bin width, which simplifies things a little bit, but R doesn’t give up the frequency table quite so easily. To get that, I had to create a variable containing all of the cut points that marked the bin boundaries and another one that assigned each value in the original data to a bin. Then I had to populate a third variable with the count frequencies within each cut range and finally bring the bins and counts together in a single table. It sounds like a lot but it’s really only a 4-line script:

T-Test: Are Averages from 2 groups the same?

It’s a common enough question and the t-test is one way to answer it. In this case we want to know if male servers and female servers receive equal tips. In Excel I have to start by separating the dataset into two gender groups and then specify the details in the T-test dialog for testing means between two samples. I also have to decide whether to use a version of the test that assumes equal or unequal variances between the two samples. I’ll skip over proving that they are equal (they are), and just show the version of the test that assumes equal variances. As with other ToolPak functions, the dialog lets me specify input and output characteristics as well as the level of significance applied to the test. The output is a simple tabulation of the test result:

This is a 2-tailed test and the P-value greater than 0.05, so I accept the null hypothesis and conclude that there is no difference between the tips received by male and female servers.

The R equivalent is a single command that splits the dataset into two groups according to the variable “sex”. The output includes a reminder about the statistical hypothesis (just in case I have forgotten) and estimates the confidence interval for the difference in the means between the two samples.

Correlation

More often than not a dataset has more than one variable, and in the early stages of exploratory analysis it’s common to ask whether or not there is a relationship between any pairs of variables in the set. Correlation is one way to answer that question, and “economics” is a sample datasets packaged with the R’s ggplot2 package that demonstrates this nicely.

The dataset includes economic indicators collected over a nearly 50-year period. In this case the analysis question is whether or not there is a relationship between personal consumption expenditures (represented as pce) and the personal savings rate (psavrt). Since money is something a person can either save or spend the intuitive answer would be a strong, inverse relationship between spending and saving. Both R and Excel offer simple functions that answer the question by calculating the correlation coefficient for this variable pair as -0.84, confirming what we expected.

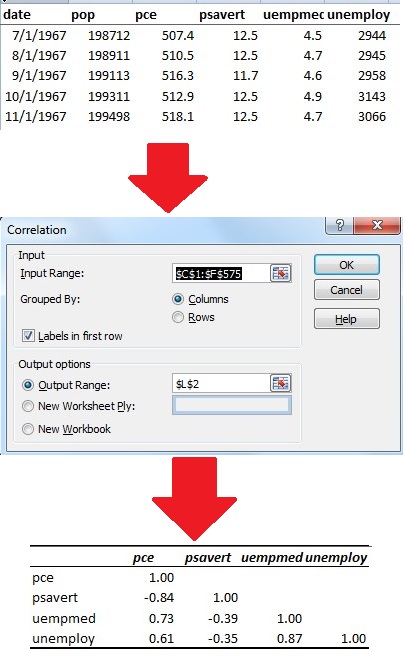
But are there any other relationships between pairs of variables? R provides a quick answer in the form of a correlation table using the same function used for the single variable pair. The only change is specifying all of the variables at once, using position within the table to reference them.

The procedure in Excel is similar but there’s an extra step. Where R let me specify the columns to include in the analysis by position, Excel required them to be adjacent to each other. Not a big deal with a small dataset like this one (574 rows and 6 columns) but potentially a problem with a large dataset. Once the columns were in the right order, I just specified the input and output ranges and Excel did the rest.

Linear Regression

Correlation tells whether or not there is some kind of relationship between two variables but in itself it has no predictive value. If I want to do predictive modeling then for some input variable, x, I’m looking for an expected response, y. The simplest version is a straight-line relationship that is the best-fit path through a dataset that has two variables.

The ggplot2 package in R contains a sample data set called father.son, which illustrates how to do simple linear regression. It contains over 1,000 sets of paired observations of the heights of fathers and sons. If I’m asking whether or not the father’s height can be used to predict the son’s it’s helpful to start by visualizing the data. The ggplot function gives me a scatter plot of the data, the best fit line through the data and an uncertainty band around it:

 

To get the equation for the best-fit line I needed the lm function, which I used to populate a variable called heightsLM with the results of the analysis:

This expresses a linear relationship:

Son Height = 33.89 inches + 0.51 x Father Height

There’s plenty of scatter in the data so if I’m a prudent modeller I also want to know more about how much confidence to put in the accuracy of the prediction. As it turns out the lm function also calculates a series of statistics that I can display using the summary function:

The result table can be a little intimidating at first glance but it is giving me an idea of how far to trust the quality of the prediction that comes from the equation. The low p-value associated with the F statistic tells me that there is a significant linear relationship between the father’s height and the son’s height, but the value of R-squared tells me that on average, variation in the heights of fathers explains only a quarter of the variation in the heights of their sons. As a predictive model it has some limitations, but R gave me both both the model and an evaluation of its quality with very little effort.

In Excel, the process is equally straightforward. Having exported the dataset from R in the form of a CSV file I could open it in Excel and then use the Regression option from the Analysis ToolPak to get both the scatter plot and the regression statistics in a single step:

In addition to the usual specification of input and output ranges, the dialogue offers options about chart outputs and other things that may be useful in evaluating the predictive value of the regression model. The output consists of an ANOVA table that gives me the same statistical summary about the quality of fit that R provided. It also goes a little further, calculating the confidence limits for all of the coefficients calculated for the regression equation. In the interest of full disclosure, this is prettier than the raw Excel output. To make it more readable I re-scaled the chart to just show the range of the data values (something R did automatically); added the regression equation using the right-click local menu and applied some formatting to the ANOVA table.

I could go on but by now you should have the idea. Both R and Excel have very accessible sets of tools for basic statistics, even for a beginner. If you are an experienced Excel user and you’re new to R, an introductory handbook like R for Everyone by Jared Lander is a good way to jump-start the process. Another great resource is R for Excel Users by John Taveras. If your needs extend to more advanced statistical work, R has a rich tool kit but it takes work, especially if you want presentation quality data visualization. But that’s a topic for another time.